TM 1-1500-204-23-2
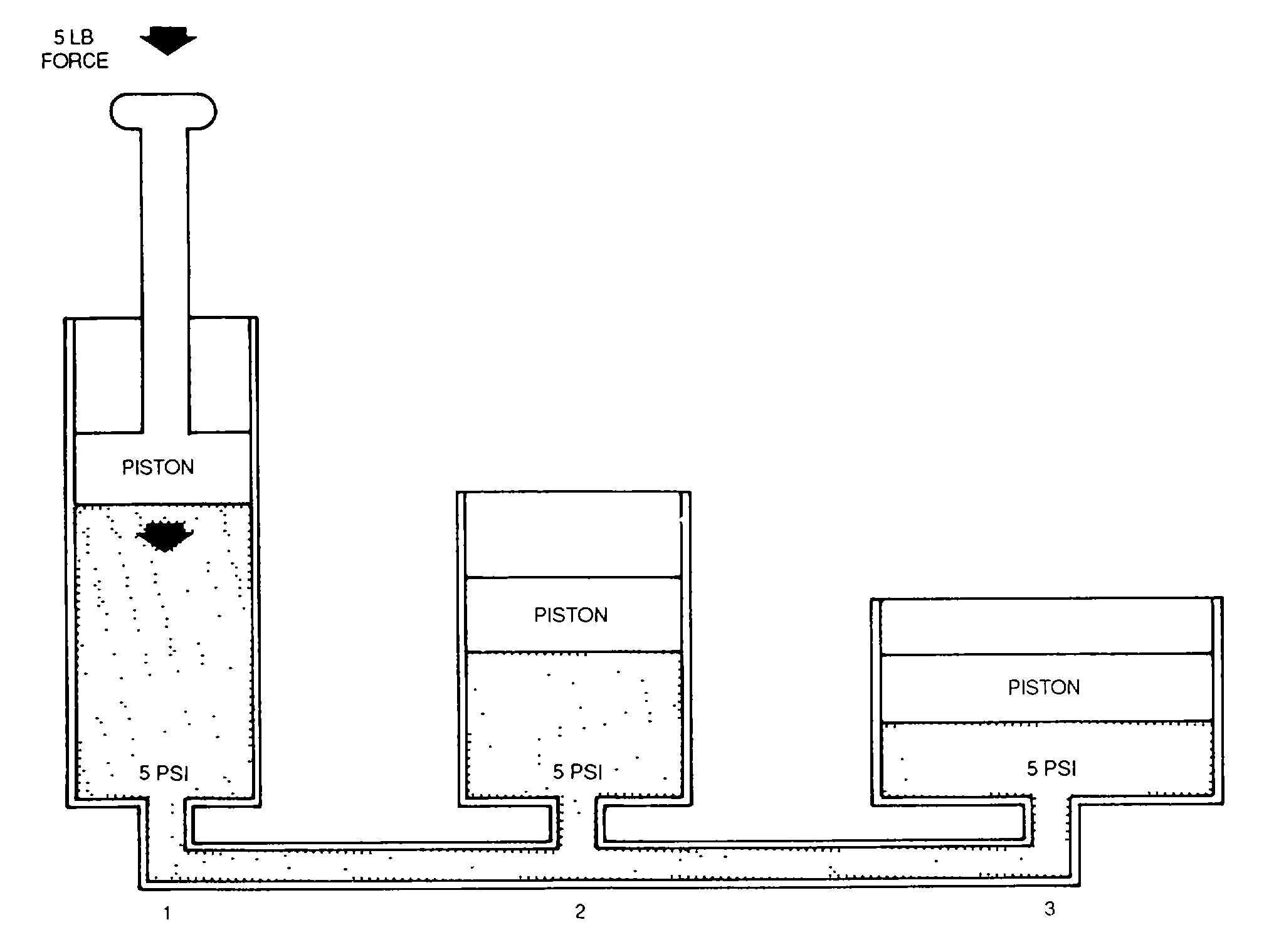
Figure 2-3. Pascal's Law
(1)
Principle. In hydraulics, mechanical advantage can be explained as the ratio between two pistons with
regard to the factors of area and force. In figure 2-4, you see a graphic illustration of this principle. Note the differences
in the areas of the small and large pistons. This difference in size is the means by which mechanical advantage is
obtained when a 50-pound force is applied to the small pistons, the fluid pressure shows 25 psi on the gauge, but 25 psi
acting on the large piston gives an upward force of 250 pounds. This gain in force (from 50 pounds to 250 pounds) is
attained by increasing the surface area of the output piston. It is important to note that this 5-to-1 ratio does not change if
the pounds per square inch change. If, for example, the input force were limited to 20 psi or raised to 30 psi, the forces
involved would obviously change but the ratio between the forces would still be 5 to 1.
(2)
Application. An example of how to apply mechanical advantage is shown in figure 2-5. Here we want
to find just how big the large piston must be to raise an 800-pound weight. Let us assume that we must raise the 800-
pound weight by applying a 40-pound force to the 4-square-inch piston. The mechanical advantage in this case is 20-800
pounds divided by 40 pounds and is expressed as the ratio 20 1. Multiplying 20 times 4 square inches (area of the small
piston), we find that the area of the large piston should be 80 square inches. Mechanical advantage also applies to the
distance the piston moves, or length of stroke. Assuming that the large piston must move 10 inches, multiplying this
factor by 20 gives 200 inches as the length of stroke for the small piston. Of course, it would not be feasible for the small
piston to move that far on a single stroke. Therefore, the small piston must move through a series of short repeated
strokes.
2-3